Dynamic and thermodynamic crossover phenomena in supercritical fluids

 

When the temperature and pressure are increased beyond the liquid-gas critical point, the vapor-liquid phase boundary collapses and a single phase of supercritical fluid (SCF) emerges. SCF is known to exhibit both macroscopic and microscopic anomalies: the former is the salient dynamic and thermodynamic crossover in the supercritical phase diagram, and the latter is the inhomogeneous distribution of molecules. These exotic characters render them attractive as green solvents to be used in the industry, including separation, extraction, and reaction. However, the question as to what basic physics underlies these microscopic and macroscopic anomalies remains open. In this project, using molecular simulation and data-driven analysis techniques, we developed novel theoretical frameworks to describe the anomalies of the SCF, where the SCF is understood as an inhomogeneous mixture of liquid-like and gas-like microstates.

J. Phys. Chem. Lett. Vol. 11, Iss. 2 (2020) (Supplementary Cover)

J. Phys. Chem. Lett. Vol. 9, Iss. 22 (2018) (Supplementary Cover)

.

.

.

.

.

1. Supercritical gas-liquid coexistence in the Widom delta

The two-state nature of the SCF was first verified by a statistical mixture model. The local density distribution of supercritical carbon dioxide was well fitted to a mixture of inverse-gamma (gas-like) and normal (liquid-like) distributions [1]. The mixture model was further applied to explain the negative partial molar volume behavior of attractive solutes in the supercritical solvent, i.e. the decrease of the total volume of the system under the addition of trace amounts of solutes: the attractive solute transformed its neighboring gas-like solvents into liquid-like states, which decreased the total volume of the system [2].

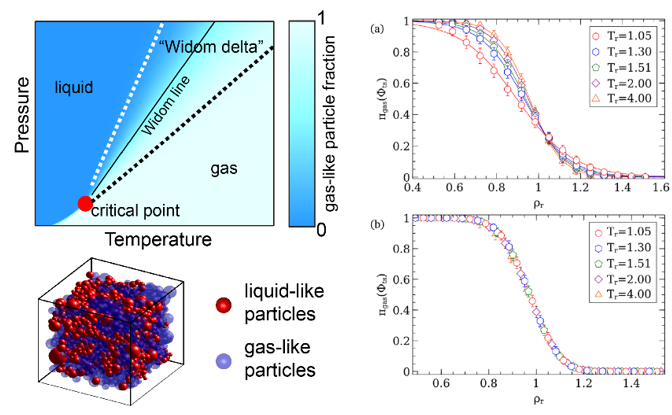
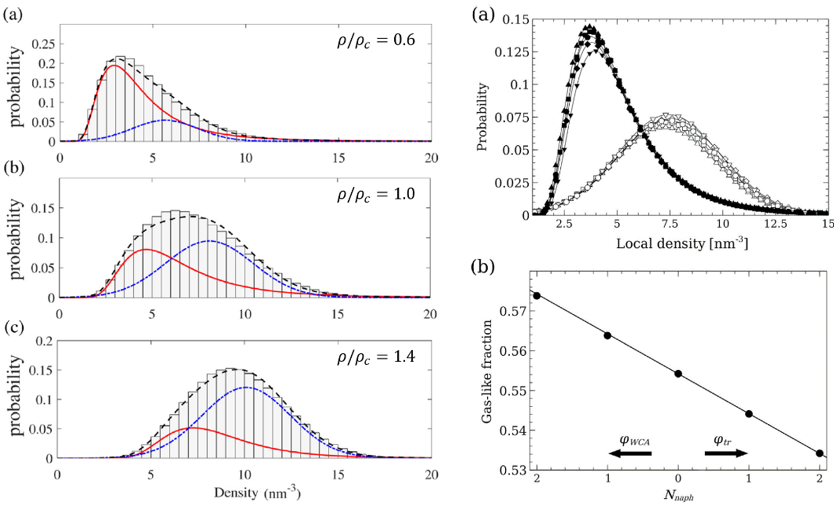The two-state coexistence of the SCF was further verified by using machine learning analysis on the local structure of near-critical and supercritical fluids. We found that the fraction of gas-like (or liquid-like) molecules in the SCF varies continuously in the supercritical condition, forming a deltoid region of coexistence. Furthermore, the loci of equal gas/liquid fraction agreed with the thermodynamic Widom line, which is conventionally described as the extension of the subcritical vapor-liquid coexistence line. Hence, the deltoid coexistence region was termed the “Widom delta” [3]. The Widom delta could also be located without resorting to machine learning methods [4].

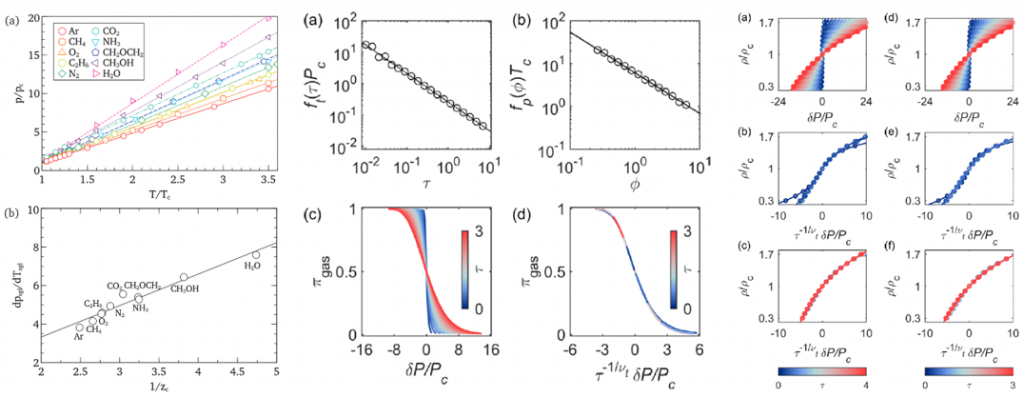
Interestingly, the Widom delta provides a material-independent framework to describe the macroscopic behavior of fluids in supercritical states. Various molecular liquids could be described by a three-parameter corresponding-state framework, where the critical compressibility is the key parameter [5]. Finally, the machine-learned gas-like fractions of different fluids could be collapsed by a universal scaling exponent, providing a universal description of the supercritical fluids hitherto unknown [6]. These results support our model of the SCF as a mixture of two interchangeable microstates, whose spatiotemporal dynamics gives rise to unique macroscopic properties.

2. Topological framework for structure-dynamics relation in supercritical fluid

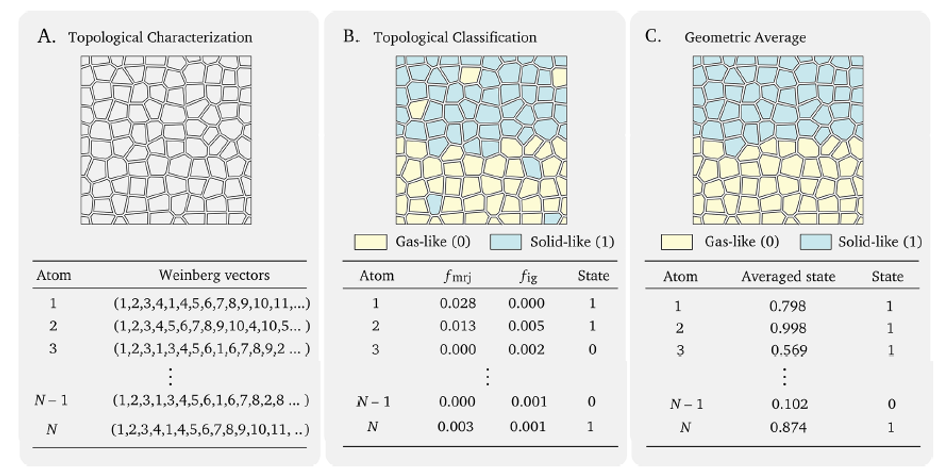
Another important dividing line of the SCF is the Frenkel line, where the ballistic motion of low-density, gas-like SCF transitions into oscillatory, liquid-like motions. Unlike the widely accepted concept of the Widom line, both the universality and the utility of the Frenkel line is under intensive debate. We first clarified the connections among pre-existing, fragmentized criteria for the Frenkel line and showed that the Frenkel line demarcates the boundary between rigid and non-rigid dynamics of fluids and cannot be related to the liquid-gas critical phenomena [7]. Then we developed a framework that exploits the topological information in the local atomic environment to show that the Frenkel line is characterized by the percolation of rigid, solid-like structures that support the propagation of rigid dynamic modes [8]. It was further verified that the topological framework can be universally employed to locate the Frenkel line in both soft-sphere and hard-sphere fluids [9]. Finally, quantifying the diversity in the graph topologies via the information entropy, we extended the Frenkel line concept to the quasi-universal description of the liquid-state physics, namely, the isomorph theory [10].

References

[1] T. J. Yoon, M. Y. Ha, W. B. Lee, and Y.-W. Lee, J. Supercrit. Fluids 119, 36—43 (2017).

[2] T. J. Yoon, M. Y. Ha, W. B. Lee, and Y.-W. Lee, J. Supercrit. Fluids 130, 364—372 (2017).

[3] M. Y. Ha, T. J. Yoon, T. Tlusty, Y. Jho, and W. B. Lee, J. Phys. Chem. Lett. 9, 1734—1738 (2018).

[4] T. J. Yoon, M. Y. Ha, W. B. Lee, and Y.-W. Lee, J. Chem. Phys. 149, 014502 (2018).

[5] T. J. Yoon, M. Y. Ha, W. B. Lee, and Y.-W. Lee, J. Chem. Phys. 150, 154503 (2019).

[6] M. Y. Ha, T. J. Yoon, T. Tlusty, Y. Jho, and W. B. Lee, J. Phys. Chem. Lett. 11, 451—455 (2020).

[7] T. J. Yoon, M. Y. Ha, W. B. Lee, and Y.-W. Lee, J. Phys. Chem. Lett. 9, 4550—4554 (2018).

[8] T. J. Yoon, M. Y. Ha, E. A. Lazar, W. B. Lee, and Y.-W. Lee, J. Phys. Chem. Lett. 9, 6524—6528 (2018).

[9] T. J. Yoon, M. Y. Ha, W. B. Lee, Y.-W. Lee, and E. A. Lazar, Phys. Rev. E 99, 052603 (2019).

[10] T. J. Yoon, M. Y. Ha, E. A. Lazar, W. B. Lee, and Y.-W. Lee, Phys. Rev. E 100, 052502 (2019).